Mrs. Mundt here! I am a 4th grade teacher at a PYP school in Minneapolis. I have a love of all things education and am especially passionate about social justice, children's literature, and inquiry in the classroom. I'm in it to inspire the hearts and minds of children!
Thursday, November 14, 2013
Khan Academy Idaho | Shelby Harris & Kuna, ID
This is the teacher I mentioned in my previous post. Thoughts?
Fractions are FUN...
...and teaching them is even more fun! Teaching them so students truly understand can also be quite difficult, so it is important that we as teachers approach this topic carefully. I learned today how much of an impact language can have on student understanding of math concepts.
I have often used the words "out of" to explain fractions: 1/4 is one out of four, 3/8 is three out of eight, 6/10 is six out of ten. This leaves students thinking that 1/4 is greater than 3/4 because 1/4 has just one piece taken out of it (leaving 3 pieces), while 3/4 has three pieces taken out of it (leaving one piece). You "take more out" with 3/4, so it most be smaller, students reason. The teachers language leaves them with the opposite answer. Fancy that! I never would have realized this on my own - what an awesome opportunity to get into the minds of my future students. Understanding a student's thought processes when making an error is the first step toward helping him or her correct that error.
As a substitute teacher, I have helped several students with problems involving fractions. Just last week, a student told me to talk in "kid language" while explaining fractions. This was humbling, as I felt I was using very clear, easy-to-understand terms. Looking back on this experience, I realize I used "out of" in my explanation. Oops.
I was trying to explain how mixed numbers and improper fractions can be used interchangeably. This student was puzzled by mixed numbers. We worked with 1 1/4. He pointed to the first 1 and then the second, very confused. "How can we have more than a whole? We have one already." I made some silly putty pies to demonstrate. By the end of our conversation, he recognized we had one whole pie and that the 1/4 was part of a second pie. This was definitely an "a-ha!" moment.
Next, I partitioned the first pie into four pieces (imagine in my graphic - I'm new to Canva and am still struggling some, though it's awesome), so we could count five total pieces to get to the improper fraction 5/4. I didn't get too far on this explanation. I could tell the student was drained from all of the hard thinking we had done. Plus, I had been so totally "in the zone" talking to this student that I had neglected the numerous raised hands and "Miss Harrison's" throughout the rest of the classroom. I decided to call it a day and went to answer the other student questions. I faced a teacher's dilemma that day: I could either focus on truly and fully explaining concepts to this one student who was struggling so, or I could brush the topic's surface while assuring everyone in the class got his or her questions at least partially answered.
Khan Academy has some amazing videos explaining fractions in a straightforward, easy-to-understand way. In the documentary Teach, a math teacher implements a model of blended learning in which students work on Khan Academy on individual computers. I think this is an awesome way for students to work at their own pace and develop a solid understanding of topics before moving on. It would, however, be hard as a teacher to relinquish this "control," as this model isn't generally what we picture when we think of teaching. As great as this program seems, I would still be sure to pull struggling students aside in order to enhance their understanding with manipulatives, especially for a fundamental topic like fractions.
I am happy my struggling student understood at least a fraction (punny, I know) of what he needed to know the other day, but I am frustrated that I couldn't help him more. Has anyone else been in this boat? Please share!
Saturday, November 9, 2013
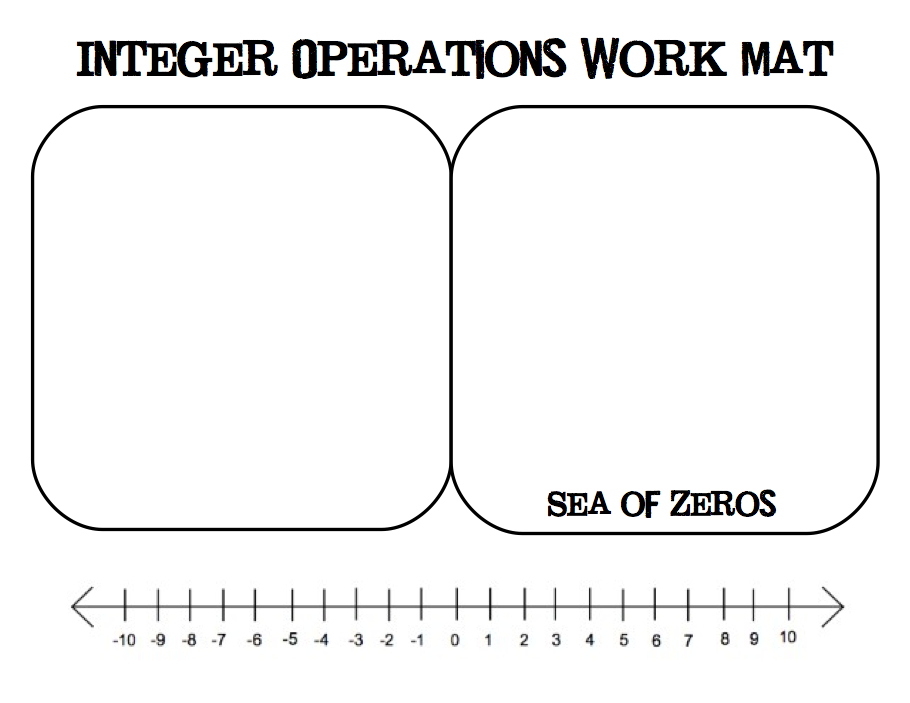
The sea of zeros...adding and subtracting integers with colored counters!
Adding and subtracting integers with counters is such a fantastic idea. The woman in this video uses little pieces of paper as counters, which works also. She puts numerous positive-negative counter pairs together to create a "Sea of Zeros" that students can access when doing integer addition and subtraction.
This blogger places the "Sea of Zeros" on an organized "work mat" template for students. The work mat also includes 1) a place for positive and negative counters not in zero pairs and 2) a number line. Students can see clearly that the result is the same whether obtained through number line or integer counters. I really like the organized format:
Unfortunately, I haven't had the opportunity to watch this method in action while subbing. I've gotten to teach equivalent fractions (multiple times), so hopefully this will be covered in future chapters so I can discuss this some.
Subbing has been challenging. Fortunately, I was able to sub in the same second grade class for four days. It was so helpful getting to know the students. It's near to impossible to run a classroom without knowing student names. On the first day, I used a lot of "Hey buddy," and "Dear, can you ____." The third day was the best. I used a "magic wand" to give out points for attentiveness, kindness, respect, etc. and take away points for talking out of turn, being off talk, disrespect, etc. Whole class points were available, as well, for outstanding behavior. These were exciting to give.
I subbed in Kindergarten again, although I had previously decided Kindergarten wasn't for me. This experience was better but wasn't without its share of challenges. Math time consisted of counting songs 1-100 and numbers in the teens. Love the energy these little guys produce.
That's all for now! Keep those hearts and minds a'bloomin'!
-Miss Elizabeth
That's all for now! Keep those hearts and minds a'bloomin'!
-Miss Elizabeth
Tuesday, October 22, 2013
Place Value Cups
I'm going to devote today's blog to a topic I struggle greatly with: Place Value. In our elementary math class, we have learned of a few different number systems: Egyptian, Babylonian, and Mayan, to name a few. Understanding these numbers systems greatly enhanced my understanding of our number system and its use of place value. It also helped me understand the struggle students may undergo when trying to comprehend our own Base 10 system. Although I won't look at these other number systems in today's blog post, I highly recommend examining them and sharing them with your students.
Minnesota's Math Standards regularly refer to the importance of understanding place value. This basic understanding, which feels not-so-basic when you're new to it, is crucial in efficiently undergoing mathematical operations. A student must understand place value in order to truly understand and utilize common short algorithms used for addition, subtraction, multiplication, and division.
The following tool is a neat manipulative to help to students understand place value (from http://suedowning.blogspot.com):
Sue Downing cites many uses of the cups:
"We use the cups to:
understand place value
practice counting forward and backward
learn the names of large numbers
decompose numbers to expanded form"
I made my own set of cups to try this out, and I found they were most useful for decomposing numbers to expanding form, which allows for a greater understanding of relationship between digits and their place value. By pulling out the thousands cup, I understood that a 1 in the thousands place is not 1 but rather 1,000.
However, the cups do not permit students to experiment with different representations of the same numbers as readily as other manipulatives do.
For example, we know that ten ones are equivalent to one ten. Twelve tens are the same as one hundred and two tens. Four hundred can also be expressed as 40 tens. Base 10 blocks are far more useful for demonstrating this than place value cups, as students are able to actually, physically "trade in" ten ones for one ten (or whatever the exchange is). Developing this knowledge is necessary for understanding and using algorithms.
With the cups, once students reach "10," they have to change the tens digit to 1 and the ones digit to 0. We know that ten ones is the same as one ten, but students may not understand this relationship. Nor are they able to understand and explore more abstract representations of numbers that base ten blocks allow.
Thoughts? Does anyone know of other unique manipulative for learning about place value? Have those manipulatives been effective with students?
Minnesota's Math Standards regularly refer to the importance of understanding place value. This basic understanding, which feels not-so-basic when you're new to it, is crucial in efficiently undergoing mathematical operations. A student must understand place value in order to truly understand and utilize common short algorithms used for addition, subtraction, multiplication, and division.
The following tool is a neat manipulative to help to students understand place value (from http://suedowning.blogspot.com):
Sue Downing cites many uses of the cups:
"We use the cups to:
understand place value
practice counting forward and backward
learn the names of large numbers
decompose numbers to expanded form"
I made my own set of cups to try this out, and I found they were most useful for decomposing numbers to expanding form, which allows for a greater understanding of relationship between digits and their place value. By pulling out the thousands cup, I understood that a 1 in the thousands place is not 1 but rather 1,000.
However, the cups do not permit students to experiment with different representations of the same numbers as readily as other manipulatives do.
For example, we know that ten ones are equivalent to one ten. Twelve tens are the same as one hundred and two tens. Four hundred can also be expressed as 40 tens. Base 10 blocks are far more useful for demonstrating this than place value cups, as students are able to actually, physically "trade in" ten ones for one ten (or whatever the exchange is). Developing this knowledge is necessary for understanding and using algorithms.
With the cups, once students reach "10," they have to change the tens digit to 1 and the ones digit to 0. We know that ten ones is the same as one ten, but students may not understand this relationship. Nor are they able to understand and explore more abstract representations of numbers that base ten blocks allow.
Thoughts? Does anyone know of other unique manipulative for learning about place value? Have those manipulatives been effective with students?
"The day i passed maths"
A boy who has long struggled with math shares his passing grade with his father. He knew his father would be happy, so he set up a camera to catch his reaction. So incredibly uplifting. Every child and parent should feel this kind of joy through success in school!
Thursday, September 26, 2013
The Kindergarten substitute
I just finished a full day subbing in a Kindergarten classroom. Experiencing a lot of different feelings right now, the main one being sheer exhaustion. I forget how LITTLE kindergartners are. I have so much respect for teachers that are able to work with that many little ones every single day and still maintain their cool. It is a superhero skill! I don't know how many times I was told "Teacher, ____ hit me" or "Teacher, _____ was mean to me." I was getting so many different comments from so many different students at once that I honestly didn't know what to address first, nonetheless HOW to address them. It was adorable how they just referred to me as "Teacher." I am glad I had the opportunity to experience "a day in the life" of a Kindergarten teacher (and hang out with awesome adorable little people for a day), but I am pretty sure that I wouldn't be a good match for a long-term Kindergarten teaching position. I am eager to experience more grade levels to figure out what I'd be best fit with. So far, I've subbed in elementary special ed, middle school math, and high school special ed. It's been a pretty wide range of subjects and grades! It's kind of funny, because I've done everything but the grades that I think I ultimately want to teach, 3rd-6th.
We had a 45 minute math class toward the end of the day. The students were starting to learn about patterns, and their developing understanding was interesting for me to observe. Their understanding of what a pattern is varied immensely. They had to draw the parts of a caterpillar and create a pattern out of it. The patterns some students created were fantastic, ones such as big yellow square, little red square, big yellow, little red, etc. Other students designed some pretty rockin' caterpillars and were dang proud of their work, but the concept of pattern was missing. The article "Developing World Class Students through World Class Mathematics Standards" clearly states, "Mathematics is the science of patterns" (SciMath, 5). I know Kindergartners are only just beginning their educational journey, and it is still the beginning of the year. Math is a fast paced science, and if patterns are the key, I worry that students who struggle with them might get left behind. If a student falls behind in a subject early, will he or she remain behind his or her classmates throughout the years of schooling? I can't help but wonder and hope this isn't the case.
We had a 45 minute math class toward the end of the day. The students were starting to learn about patterns, and their developing understanding was interesting for me to observe. Their understanding of what a pattern is varied immensely. They had to draw the parts of a caterpillar and create a pattern out of it. The patterns some students created were fantastic, ones such as big yellow square, little red square, big yellow, little red, etc. Other students designed some pretty rockin' caterpillars and were dang proud of their work, but the concept of pattern was missing. The article "Developing World Class Students through World Class Mathematics Standards" clearly states, "Mathematics is the science of patterns" (SciMath, 5). I know Kindergartners are only just beginning their educational journey, and it is still the beginning of the year. Math is a fast paced science, and if patterns are the key, I worry that students who struggle with them might get left behind. If a student falls behind in a subject early, will he or she remain behind his or her classmates throughout the years of schooling? I can't help but wonder and hope this isn't the case.
Tuesday, September 24, 2013
The Counting to 10 Game
1.
2, 3, 4.
5, 6.
7, 8.
9.
...10.
...followed by a mesh of groans, laughter, and shuffling as the circle grows one person smaller.
The "Counting to 10 Game" has shown itself to be very popular in the middle school classrooms I have subbed in. Last week, I saw it played in two different classrooms, grades 6 and 7. The game reminded me instantly of the "Gold Coin Game" highlighted in my math textbook. There are two players in the "Gold Coin Game." There are 15 coins placed in a pile. On each play, a player can remove one, two, or three coins from this pile. The player who takes the last coin wins the game.
The "Counting to 10 Game" utilizes similar problem solving skills, but it isn't quite the same. Any number of students can play, and when I subbed, the whole class played. Counting student by student, the group has to count up to 10. Each player can say one, two, or three numbers in a row. The student that says the number 10 is out and is eliminated from the game. You can find a lesson plan for several variations of this game here.
The 6th grade students utilized no strategies in this game. This was apparent through the quickness of their responses. Watching the students play, I was discouraged. This could have been an awesome moment for students to practice their mathematical reasoning skills, I thought. Besides providing a nice break for students, the 10 minutes spent playing felt like wasted time.
As the game proceeded, I kept thinking to myself: I don't even know how I would strategize in this game, especially with so many players and so little time to formulate a response. I was discouraged yet again, this time by my own self-perceived incompetence. I thought back to a class reading from that week, from which I here present an excerpt:
When I reached to this paragraph, I felt inspired. Learning to engage in mathematical thought will not be easy, but I am hopeful that my struggles will help me better understand my students who will someday experience similar difficulties. Math problems such as the "Gold Coin Game" and "Counting to 10 Game" are new territory to me, and it's nice to know that I will be able to someday help my students navigate this same scary world of mathematical thought.
The next period I taught - 7th grade - was inspiring. The students were using reasoning to formulate game strategies. They would pause before they spoke, trying to predict what amount of numbers would ensure they not be eliminated their next turn. During this pause, I could all but see the gears in their brains turning. Super cool.
I found some pretty awesome math videos, and I am excited to share one with you all next blog post!
2, 3, 4.
5, 6.
7, 8.
9.
...10.
...followed by a mesh of groans, laughter, and shuffling as the circle grows one person smaller.
The "Counting to 10 Game" has shown itself to be very popular in the middle school classrooms I have subbed in. Last week, I saw it played in two different classrooms, grades 6 and 7. The game reminded me instantly of the "Gold Coin Game" highlighted in my math textbook. There are two players in the "Gold Coin Game." There are 15 coins placed in a pile. On each play, a player can remove one, two, or three coins from this pile. The player who takes the last coin wins the game.
The "Counting to 10 Game" utilizes similar problem solving skills, but it isn't quite the same. Any number of students can play, and when I subbed, the whole class played. Counting student by student, the group has to count up to 10. Each player can say one, two, or three numbers in a row. The student that says the number 10 is out and is eliminated from the game. You can find a lesson plan for several variations of this game here.
The 6th grade students utilized no strategies in this game. This was apparent through the quickness of their responses. Watching the students play, I was discouraged. This could have been an awesome moment for students to practice their mathematical reasoning skills, I thought. Besides providing a nice break for students, the 10 minutes spent playing felt like wasted time.
As the game proceeded, I kept thinking to myself: I don't even know how I would strategize in this game, especially with so many players and so little time to formulate a response. I was discouraged yet again, this time by my own self-perceived incompetence. I thought back to a class reading from that week, from which I here present an excerpt:
"Too many students preparing for elementary teaching have been less than successful mathematics students, and even those with good grades often doubt their competence. Understandably, readers of this document may feel dismay at the prospect of working with such math-anxious, if not math-phobic, undergraduates. However, those who work with them can testify that, once these prospective teachers experience their own capacities for mathematical thought, their anxiety is transformed into energy for learning."
When I reached to this paragraph, I felt inspired. Learning to engage in mathematical thought will not be easy, but I am hopeful that my struggles will help me better understand my students who will someday experience similar difficulties. Math problems such as the "Gold Coin Game" and "Counting to 10 Game" are new territory to me, and it's nice to know that I will be able to someday help my students navigate this same scary world of mathematical thought.
The next period I taught - 7th grade - was inspiring. The students were using reasoning to formulate game strategies. They would pause before they spoke, trying to predict what amount of numbers would ensure they not be eliminated their next turn. During this pause, I could all but see the gears in their brains turning. Super cool.
I found some pretty awesome math videos, and I am excited to share one with you all next blog post!
Wednesday, September 18, 2013
All I have is time...
I am frustrated by the lack of subbing opportunities so far. I'm so thankful for the opportunity to sub while I wait to get licensed. I just wish there were more jobs posted.
I decided I wanted to be a teacher about a year ago, and ever since, I have been working on an extensive list of prerequisites for the program I want to apply for. Now, I just want to get in there and TEACH. It frustrates me beyond belief that I'm just not able to have my own classroom right now, and no amount of proactiveness or passion can hasten the process. I have to go through the steps: get in a program, take the necessary classes and go through the work to get licensed.
I guess the way I need to see it is that all of this preparation and patience is going to make me that much more of a passionate, well-informed teacher. Not being able to get in the classroom while I so thirst for those teaching experiences pushes me to reach for any material related to education that I can get my hands on. I've had so much time to research education from a range perspectives online, in-person, and in-text - time that I doubt many teachers have when they are actually in the classroom, due to the crazy-busyness that is the life of a teacher. Waiting so long to teach has pushed me to truly reflect upon the type of classroom I want to have and the type of teaching I want to do in order to achieve the best environment and experience for my students. This is one thing I am able to be thankful for.
In the words of Mat Kearney (my favorite artist), "Nothing worth anything ever goes down easy."
I decided I wanted to be a teacher about a year ago, and ever since, I have been working on an extensive list of prerequisites for the program I want to apply for. Now, I just want to get in there and TEACH. It frustrates me beyond belief that I'm just not able to have my own classroom right now, and no amount of proactiveness or passion can hasten the process. I have to go through the steps: get in a program, take the necessary classes and go through the work to get licensed.
I guess the way I need to see it is that all of this preparation and patience is going to make me that much more of a passionate, well-informed teacher. Not being able to get in the classroom while I so thirst for those teaching experiences pushes me to reach for any material related to education that I can get my hands on. I've had so much time to research education from a range perspectives online, in-person, and in-text - time that I doubt many teachers have when they are actually in the classroom, due to the crazy-busyness that is the life of a teacher. Waiting so long to teach has pushed me to truly reflect upon the type of classroom I want to have and the type of teaching I want to do in order to achieve the best environment and experience for my students. This is one thing I am able to be thankful for.
In the words of Mat Kearney (my favorite artist), "Nothing worth anything ever goes down easy."
Labels:
classroom,
educating youth,
education,
elementary education,
jobs,
passion,
patience,
professional development,
subbing,
substitute teacher,
teach,
teacher,
teacher preparation,
teaching,
teaching licensure
Sunday, September 15, 2013
Cross-curricular teaching
In addition to taking Math for Elementary Teachers, I am also currently taking Children's Literature and PE for Elementary Teachers. Having multiple classes related to one broad topic (elementary education, in this case) allows for some pretty exciting connections. I did this a lot with my psych, natural science, and liberal arts courses in undergrad. I am a huge fan of "making connections," and studies have shown that students benefit from this, as well!
Interdisciplinary/cross-curricular teaching has been shown to engage students by allowing them to see the importance and value of topics taught. I am new to the concept but very intrigued. It sounds like an important element of this type of teaching is explaining to children what you are doing with cross-curricular teaching and how it will benefit them.
http://adyteaching.blogspot.com/2013/05/i-know-what-but-i-want-to-know-why-make.html
While browsing pinterest, I discovered math journals. I have heard of them before but haven't truly appreciated their value until now. What an awesome way to get students to reflect upon their learning, utilize reasoning skills and critical thinking in math (no automated number crunching in these things), and develop their writing skills and vocabulary across subjects. Math literacy much? I love the "My Life in Numbers" entry idea!
http://love2learn2day.blogspot.ca/2011/10/my-life-in-numbers.html
http://www.pinterest.com/pin/134052526382032083/
My PE class has made me recognize the importance of incorporating physical activity into many disciplines, math included. I am inspired to discover activities that get their students out of their desks and into their thinking caps! I am really into "Whole Brain Teaching" and hope to one day incorporate it into my classroom. The first link I posted describes it briefly at the end of the post. See video, too!
Here are some active math activities I discovered while browsing:
http://www.motheringwithcreativity.com/2013/04/adding-fun.html
http://www.pinterest.com/pin/134052526382032126/
The first game could certainly be made even more physical: by throwing balls into hoops, multiplying the balls in the basket by a certain number of jumping jacks, etc. In my PE class, we played a game where two dice were rolled and students had to calculate the sum and do that many of a certain action (i.e. squats, leap frog jumps, etc).
Share some engaging cross-curricular activities you've stumbled upon, created, or reinvented!
Interdisciplinary/cross-curricular teaching has been shown to engage students by allowing them to see the importance and value of topics taught. I am new to the concept but very intrigued. It sounds like an important element of this type of teaching is explaining to children what you are doing with cross-curricular teaching and how it will benefit them.
http://adyteaching.blogspot.com/2013/05/i-know-what-but-i-want-to-know-why-make.html
While browsing pinterest, I discovered math journals. I have heard of them before but haven't truly appreciated their value until now. What an awesome way to get students to reflect upon their learning, utilize reasoning skills and critical thinking in math (no automated number crunching in these things), and develop their writing skills and vocabulary across subjects. Math literacy much? I love the "My Life in Numbers" entry idea!
http://love2learn2day.blogspot.ca/2011/10/my-life-in-numbers.html
http://www.pinterest.com/pin/134052526382032083/
My PE class has made me recognize the importance of incorporating physical activity into many disciplines, math included. I am inspired to discover activities that get their students out of their desks and into their thinking caps! I am really into "Whole Brain Teaching" and hope to one day incorporate it into my classroom. The first link I posted describes it briefly at the end of the post. See video, too!
Here are some active math activities I discovered while browsing:
http://www.motheringwithcreativity.com/2013/04/adding-fun.html
http://www.pinterest.com/pin/134052526382032126/
The first game could certainly be made even more physical: by throwing balls into hoops, multiplying the balls in the basket by a certain number of jumping jacks, etc. In my PE class, we played a game where two dice were rolled and students had to calculate the sum and do that many of a certain action (i.e. squats, leap frog jumps, etc).
Share some engaging cross-curricular activities you've stumbled upon, created, or reinvented!
Thursday, September 12, 2013
Polya in action
Last post, I asked, "What does it mean to be math literate?"
Unfortunately, I myself do not yet have an answer for this question. I already see this will be an ongoing investigation throughout this semester and beyond.
I began my investigation this morning, as a substitute teacher in a high school special education classroom. I subbed for two classes - pre-algebra foundations (9th and 10th grade) and consumer math (11th and 12th).
In the first class, we worked with exponents. The majority of the students were completely stumped on the last problem, and I had the chance to utilize some of the problem solving strategies we have been working on in this course. I utilized Polya's Problem-Solving Principles to teach students how to tackle the problem.
http://www.learnlogic.net/design/polyas-problem-solving-process/
- - - - - - - - - -
Here is problem:
Figure out the relationship between the numbers in the top and bottom rows of the provided chart. Then, write a variable expression to determine the bottom number when the top number is n.
1) Understand the problem: I encouraged students to first read the question thoroughly, as many of them hadn't yet done that. I explained terminology, including what it meant to write a variable expression. I explained what n is. I helped the students understand what we were trying to accomplish.
2) Devise a plan: I made it clear to students which relationship we needed to understand in order to solve the problem. I pointed to numbers in the chart provided to make this very clear. We chose guess and check as a strategy.
The students struggled to understand that n can be any number and that we can use the variable expression with n that we are trying to establish in order to find the bottom value for any top value. We decided to first establish the relationship between top and bottom, as this would essentially give us our variable expression.
3) Carry out the plan: Students looked for the relationship between the top and bottom numbers. We started with 2. Consistent with that particular column, many students suggested that the bottom number was 8 times the top number. I told the students to check the trend in the other columns. They realized quickly that this didn't work with the other top numbers.
I asked students what the worksheet focused on, and they answered exponents. I hinted that the relationship between the two numbers likely had to do with this topic. They tested out different exponents (2^2, 2^3, etc.) before discovering that 2^4 equals 16. They tested 3 and 4 in order to determine if this pattern held true, which it did. The top number to the 4th power gave us the bottom number. Therefore, if the top number is any number n, the bottom must be n^4.
4) Look back: We didn't look into different strategies we could have used, but we took the problem one step further. There was still some confusion over the function of n that had to be addressed. Some students filled in 4 for the question mark rather than n^4. I wanted students to understand that any number can be substituted for n, so I had them plug in 5 and calculate what the bottom value would be. Having them plug in other non-sequential values, as well, could help eliminate some confusion. I am not sure how much these students have talked about variables yet, either, so further discussion on their function would certainly help a lot.
- - - - - - - - - -
So back to my initial question - what does it mean to be math literate? Today's experience has led me to incorporate a few elements into my personal understanding of "math literacy:"
-Being able to use reasoning skills on a problem that is initially puzzling. Equipped with Polya's strategies, I was able to help students in the pre-algebra class explore this skill.
-Being able to APPLY skills to your everyday life. The consumer math class worksheet today focused on calculating daily wage using hourly wage and hours worked. This is most definitely a relevant skill, as many of the students in this class are seniors soon to experience the working world. This is way more important than just crunching out values.
I will write more about this subbing experience in a future post. I look forward to share my teaching experiences with my readers!
Unfortunately, I myself do not yet have an answer for this question. I already see this will be an ongoing investigation throughout this semester and beyond.
I began my investigation this morning, as a substitute teacher in a high school special education classroom. I subbed for two classes - pre-algebra foundations (9th and 10th grade) and consumer math (11th and 12th).
In the first class, we worked with exponents. The majority of the students were completely stumped on the last problem, and I had the chance to utilize some of the problem solving strategies we have been working on in this course. I utilized Polya's Problem-Solving Principles to teach students how to tackle the problem.
http://www.learnlogic.net/design/polyas-problem-solving-process/
- - - - - - - - - -
Here is problem:
Figure out the relationship between the numbers in the top and bottom rows of the provided chart. Then, write a variable expression to determine the bottom number when the top number is n.
1
|
2
|
3
|
4
|
…
|
n
|
1
|
16
|
81
|
256
|
…
|
?
|
1) Understand the problem: I encouraged students to first read the question thoroughly, as many of them hadn't yet done that. I explained terminology, including what it meant to write a variable expression. I explained what n is. I helped the students understand what we were trying to accomplish.
2) Devise a plan: I made it clear to students which relationship we needed to understand in order to solve the problem. I pointed to numbers in the chart provided to make this very clear. We chose guess and check as a strategy.
The students struggled to understand that n can be any number and that we can use the variable expression with n that we are trying to establish in order to find the bottom value for any top value. We decided to first establish the relationship between top and bottom, as this would essentially give us our variable expression.
3) Carry out the plan: Students looked for the relationship between the top and bottom numbers. We started with 2. Consistent with that particular column, many students suggested that the bottom number was 8 times the top number. I told the students to check the trend in the other columns. They realized quickly that this didn't work with the other top numbers.
I asked students what the worksheet focused on, and they answered exponents. I hinted that the relationship between the two numbers likely had to do with this topic. They tested out different exponents (2^2, 2^3, etc.) before discovering that 2^4 equals 16. They tested 3 and 4 in order to determine if this pattern held true, which it did. The top number to the 4th power gave us the bottom number. Therefore, if the top number is any number n, the bottom must be n^4.
4) Look back: We didn't look into different strategies we could have used, but we took the problem one step further. There was still some confusion over the function of n that had to be addressed. Some students filled in 4 for the question mark rather than n^4. I wanted students to understand that any number can be substituted for n, so I had them plug in 5 and calculate what the bottom value would be. Having them plug in other non-sequential values, as well, could help eliminate some confusion. I am not sure how much these students have talked about variables yet, either, so further discussion on their function would certainly help a lot.
- - - - - - - - - -
So back to my initial question - what does it mean to be math literate? Today's experience has led me to incorporate a few elements into my personal understanding of "math literacy:"
-Being able to use reasoning skills on a problem that is initially puzzling. Equipped with Polya's strategies, I was able to help students in the pre-algebra class explore this skill.
-Being able to APPLY skills to your everyday life. The consumer math class worksheet today focused on calculating daily wage using hourly wage and hours worked. This is most definitely a relevant skill, as many of the students in this class are seniors soon to experience the working world. This is way more important than just crunching out values.
I will write more about this subbing experience in a future post. I look forward to share my teaching experiences with my readers!
Tuesday, September 3, 2013
Math literate?
Hello readers! I welcome you to my blog, Blooming Hearts and Minds. To begin, a brief introduction of myself and my purpose for writing:
My name is Elizabeth Harrison. I am a 23-year-old college graduate, specializing in Psychology and Hispanic Studies. My intention after graduating was to go into Child Clinical Psychology. I have always connected extraordinarily well with children, and I knew I wanted to fulfill a role in which I could encourage youth directly. I applied last minute for three clinical psych programs, interviewed with one, and was accepted by none. I took the "rejection" in stride and let this "door closing" lead me to my next adventure - Minnesota Reading Corps (MRC).
Love. Head over heels love.
In this position, I worked directly with upwards of 30 bright young minds over the course of the school year. I fell in love with the school I served in and developed an intense passion for education, particularly literacy education. I found myself checking out book after book covering debated topics of education and theories on how to best connect with students. I decided during this year of service that teaching was the path for me. I honestly feel it is not just my chosen career but rather, my vocation (Parker Palmer is one of my favorite author, thanks to a liberal arts education bountiful in theology and philosophy emphases).
I am taking courses right now that allow me to work toward my license in Elementary Education. One of those courses is Math of Elementary Teachers I, a course which is requiring me to create and update this blog. I have always wanted to have a blog of my own, so I am grateful for this mandatory jumpstart.
As mentioned, my experiences through MRC encouraged me to explore literacy education. By literacy, I am referring to the ability to read, write, think critically, etc. - all elements we commonly think of when this term "literacy" is thrown around. Just a week in, my Math for Elementary Teachers course is prompting me to discover alternative facets of literacy - math literacy, to name one. I am still trying to discover what exactly "math literacy" refers to.
To you, what does it mean to be "math literate?" How can we teach our students to become "math literate?"
I look forward to exploring this question among others with input from those in my class and the education world as a whole. I appreciate any feedback and look forward to this learning experience with all of you!
My name is Elizabeth Harrison. I am a 23-year-old college graduate, specializing in Psychology and Hispanic Studies. My intention after graduating was to go into Child Clinical Psychology. I have always connected extraordinarily well with children, and I knew I wanted to fulfill a role in which I could encourage youth directly. I applied last minute for three clinical psych programs, interviewed with one, and was accepted by none. I took the "rejection" in stride and let this "door closing" lead me to my next adventure - Minnesota Reading Corps (MRC).
Love. Head over heels love.
In this position, I worked directly with upwards of 30 bright young minds over the course of the school year. I fell in love with the school I served in and developed an intense passion for education, particularly literacy education. I found myself checking out book after book covering debated topics of education and theories on how to best connect with students. I decided during this year of service that teaching was the path for me. I honestly feel it is not just my chosen career but rather, my vocation (Parker Palmer is one of my favorite author, thanks to a liberal arts education bountiful in theology and philosophy emphases).
I am taking courses right now that allow me to work toward my license in Elementary Education. One of those courses is Math of Elementary Teachers I, a course which is requiring me to create and update this blog. I have always wanted to have a blog of my own, so I am grateful for this mandatory jumpstart.
As mentioned, my experiences through MRC encouraged me to explore literacy education. By literacy, I am referring to the ability to read, write, think critically, etc. - all elements we commonly think of when this term "literacy" is thrown around. Just a week in, my Math for Elementary Teachers course is prompting me to discover alternative facets of literacy - math literacy, to name one. I am still trying to discover what exactly "math literacy" refers to.
To you, what does it mean to be "math literate?" How can we teach our students to become "math literate?"
I look forward to exploring this question among others with input from those in my class and the education world as a whole. I appreciate any feedback and look forward to this learning experience with all of you!
Subscribe to:
Comments (Atom)